[ML] 정보이론: Entropy, KL Divergence, Mutual Information(MI)

💡 본 문서는 '[ML] 정보이론: Entropy, KL Divergence, Mutual Information(MI)'에 대해 정리해놓은 글입니다.
~~~정리하였으니 참고하시기 바랍니다.

1. Entropy

엔트로피는 불확실성을 의미한다. 과학에서 쓰이는 엔트로피를 보면 동일한 부피에서 고체의 엔트로피는 낮고 기체의 엔트로피는 높으며,  낮은 곳에서 높은 곳으로 흐르는 성질이 있다. 머신러닝을 위한 수학에서도 엔트로피는 같은 의미로 쓰인다. 모델을 학습하는 것은 결국 확률을 모델링하는 것이 되는데, 해당 분포가 불확실할수록 엔트로피는 높아진다. 

예를 들어 어떤 X가 있는데, 이 X는 초록사과(X=0)인지 빨간사과(X=1)인지에 대한 정보를 갖고 있는 확률 분포라고 생각해 보자. 첫 번째로 X1를 6개의 원소로 이루어진 집합이라 생각해 보자. X1 = {0,0,0,1,1,1}로 빨간 사과 3개, 초록사과 3개가 들어있으므로 이 X1를 '이 친구는 특정한 색을 지닌 사과의 집합이야!'라고 말하기는 불확실하다. 불확실하기 때문에 엔트로피가 높다는 의미다. 반대로 X2= {1,1,1,1,1,0}으로 빨간 사과 5개와 초록사과 1개로 이루어졌다면, 이 X는 빨간 사과의 집합일 확률이 높아진다. 즉 엔트로피가 높다는 것은 해당 확률 분포로 유의미한 결과를 도출하기 어렵다는 것이다. 

이렇듯 X의 확률 분포가 비슷비슷해서 불확실성이 높다면 엔트로피(H)가 높고, 반대일 경우는 H가 낮다. 이를 수식으로 나타내면 다음과 같다. 

엔트로피를 다른 식으로도 유도해 생각할 수 있는데, 그 방법은 source-code theory다. 분포 X3가 있는데, 이 분포를 압축하고 싶다고 하자. X3= {1,1,1,1,1,1}라면 X3은 위의 X1, X2를 압축하는 것 보단 쉬울 것이다. 굉장히 단순하게 X3을 압축한다면 "'1'이 '6'개" 라는 정보를 담아야 할 것이다. 반면 X1은 "'0'이 '3'개, '1'이 '3'개"라는 정보로 압축해야 한다. X3을 압축하는 게 더 쉬워 보인다. 실제로 H(X3) = 0 으로 엔트로피 값이 작다. 

Cross Entropy (CE)

위에서 X의 엔트로피 H(X)를 구해보았다. 이번에는 2개 확률 분포의 엔트로피를 통해, 빨간사과를 빨간 사과로 예측했는지를 볼 것이다. 이번에 X엔 6개가 아닌 단 1개의 사과가 있다. 사과는 90%정도 빨간 색깔이며 10%정도는 초록 빛깔이 도는 사과로, p = {0.9, 0.1}로 정의한다. 이들이 빨간 사과인지 예측한 결과는 q1, q2로 나타낸다.  q1는 사과가 30%정도로 빨간 사과일 것이라 예측했다. q2는 80% 빨간 사과일 것이라 예측했다.(q2의 예측결과가 더 정확하다.) 이제 q1, q2의 엔트로피를 p와 함께 나타내보자. 

q2의 예측 결과가 더 정확했으며, 이때의 cross entropy는 q1보다 작다. CE 수식은 아래와 같다. p가 실제값, q가 예측값임을 생각하면 딥러닝에서의 cross entropy loss를 의미함을 알 수 있다.  예시를 이어서 설명하면 H(p,q1)은 p를 압축하는 의미로도 해석할 수 있다. 예측분포 q1를 기반으로 했을 때 p의 분포를 알고 싶을 때 적어도 어느 정도(source coding theory에서의 bit)를 봐야 알 수 있냐는 의미다. 압축을 위해 봐야할 bit가 많다(cross entropy가 높다)는 뜻은 그만큼 압축하기 어려우며 p와 q의 분포가 상이하다는 뜻이다. 

오늘 든 예시는 빨간사과인지 아닌지(초록사과인지)를 나타내는 이진 분류(binary classification)으로 간주할 수 있는데, bernoulli 분포를 따르는 logistic regression에서의 likelihood에 -를 곱한 값과 동일함을 알 수 있다. 즉, binary cross entropy는 NLL(Negative Log Likelihood)와 수식적으로 동일하다. 

기타 엔트로피 

Joint Entropy

Joint Entropy는 x, y가 동시에 일어날 확률을 엔트로피로 나타낸 값이다. 엔트로피는 x의 무질서함을 확인했다고 한다면, joint entropy는 동시에 발생하는 x, y의 무질서함을 확인한다. 따라서 수식은 기본 엔트로피 수식의 p(x)를 p(x,y)로 대체한 것과 같다. 

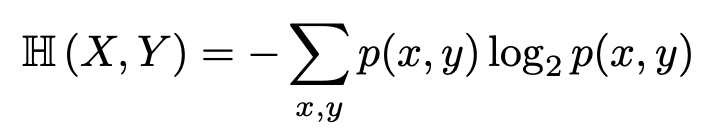
x,y가 동시에 일어날 때의 엔트로피이기 때문에 H(x,y)는 각각의 엔트로피를 더한 값보다 클 수 없다(H(X,Y) <= H(X) + H(Y)). 따라서 확률분포를 섞는다고 해서 엔트로피를 더 키울 수는 없다. 

Conditional Entropy

이번에는 엔트로피도 베이시안(ex. p(x|y) = p(x,y)/p(y))처럼 식을 변화시킬 수 있음을 확인해 볼 것이다. 조건부 엔트로피는 X가 주어졌을 때의 Y에 대한 값을 구한다. X 기반이기 때문에 이는 P(X)에 대해 p(Y|X)의 엔트로피를 구하는 것과 같다. 

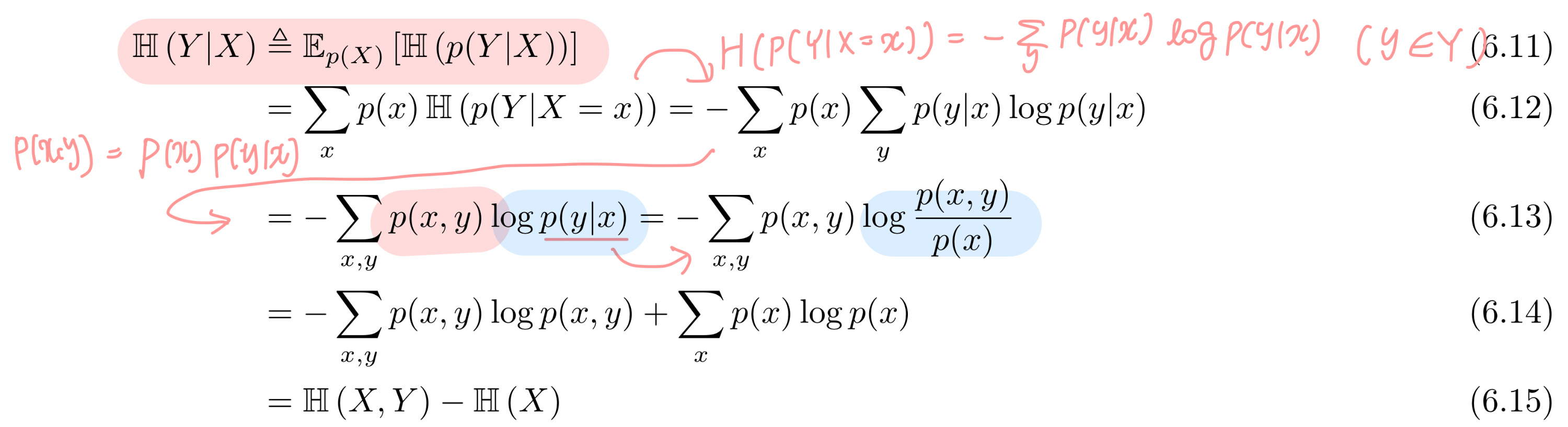
식을 전개한 결과 H(Y|X) = H(X,Y) - H(X), 즉 H(X,Y) = H(Y|X) + H(X)임을 도출했다. 여기에 X= X1, Y = X2를 대입해 보면 H(X1,X2) = H(X2|X1) + H(X1)로, chain rule이 엔트로피에도 적용됨을 알 수 있다! 

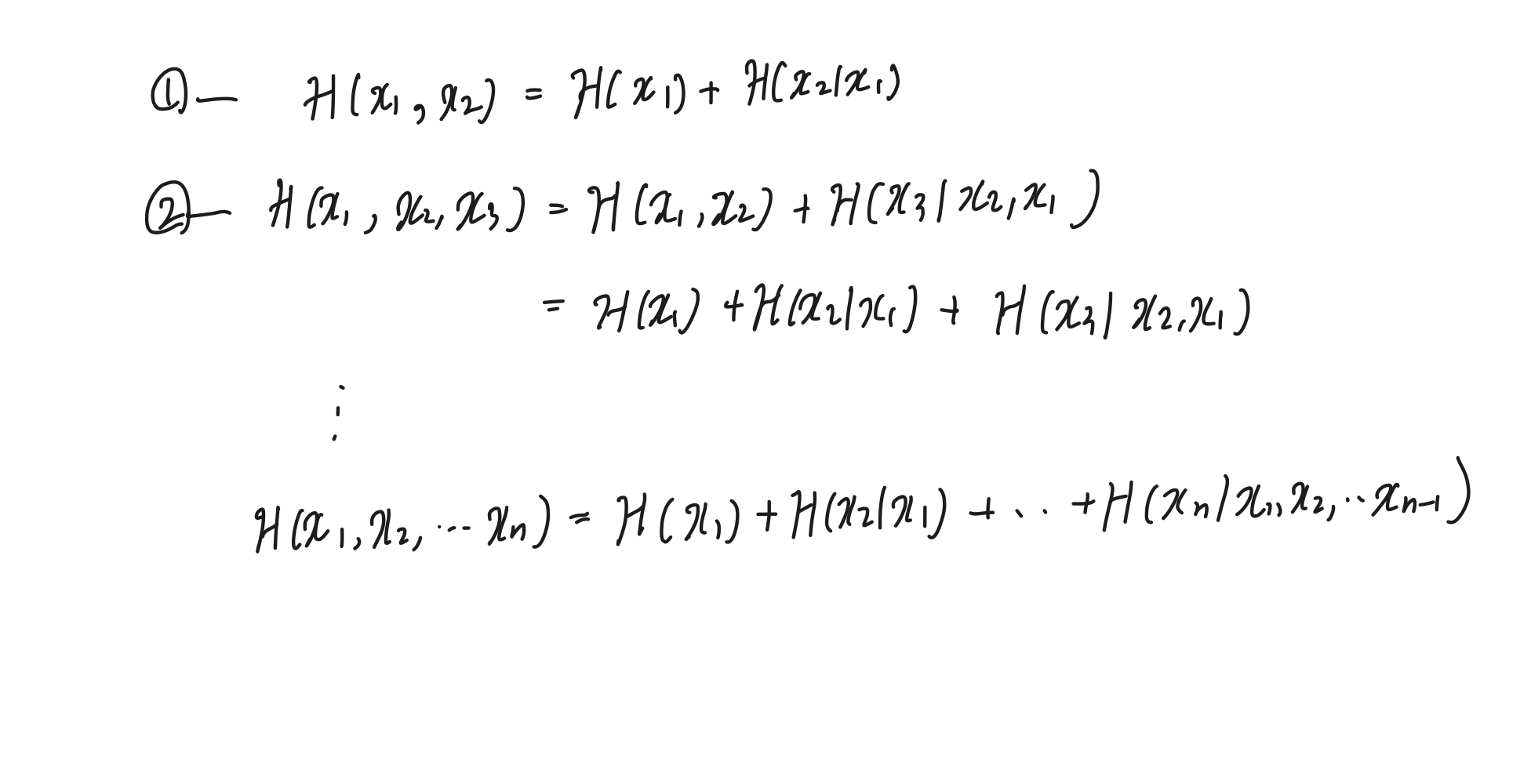
chain rule of joint entropy

chain rule을 통한 joint entropy를 다음과 같이 구할 수 있다. 

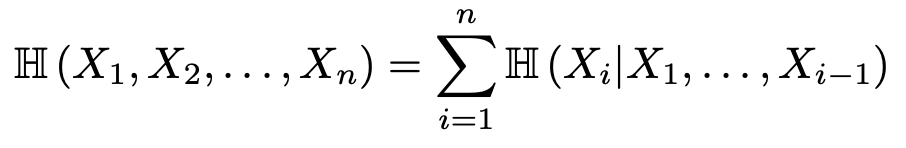
2. KL Divergence 

서로 다른 분포 p와 q가 있을 때 이 둘이 얼마나 유사한지를 재기 위해서 일반적으로 L1, L2, mahalanobis 등의 distance를 측정하고는 한다. 엔트로피를 이용해서도 p와 q의 유사성을 측정할 수 있다. KL (Kullback-Leibler) Divergence는 p와 q 간의 엔트로피를 측정하여, p와 q의 분포가 동일할수록 0에 가까워지고 그렇지 않을수록 1에 가까워진다. 수식은 다음과 같다. 

kl divergence

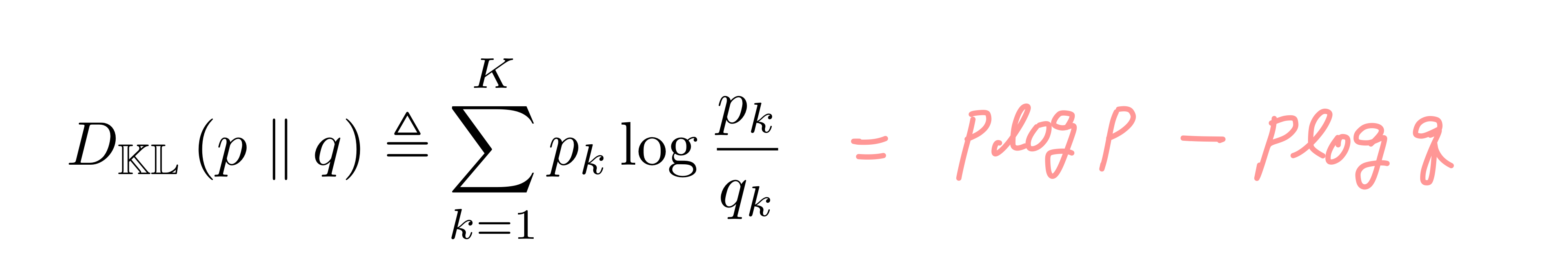
수식에서 첫번째 항은 p의 엔트로피 -H(p)를, 두 번째 항은 p,q의 크로스 엔트로피 -H(p,q)를 의미함을 알 수 있다. 크로스 엔트로피는 q 분포를 따르는 p의 데이터를 압축할 때의 lower bound를 의미했었다. 

kl divergence 2

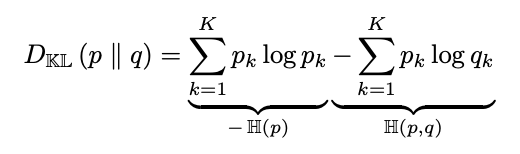
KL(p||q)의 값은 항상 0보다 작거나 같은데, 엔트로피가 log 함수로 이루어져있음을 생각한다면 당연한 결과다. log는 볼록함수기 때문에 Jensens Inequality를 통해 ∑(또는 E(평균))하면  ∑(log(x)) <= log(∑(x))를 항상 만족한다. 이를 통해 수식을 전개하면 -KL(p||q)가 항상 0보다 작거나 같음을 아래와 같이 알 수 있다.  

-KL <= 0

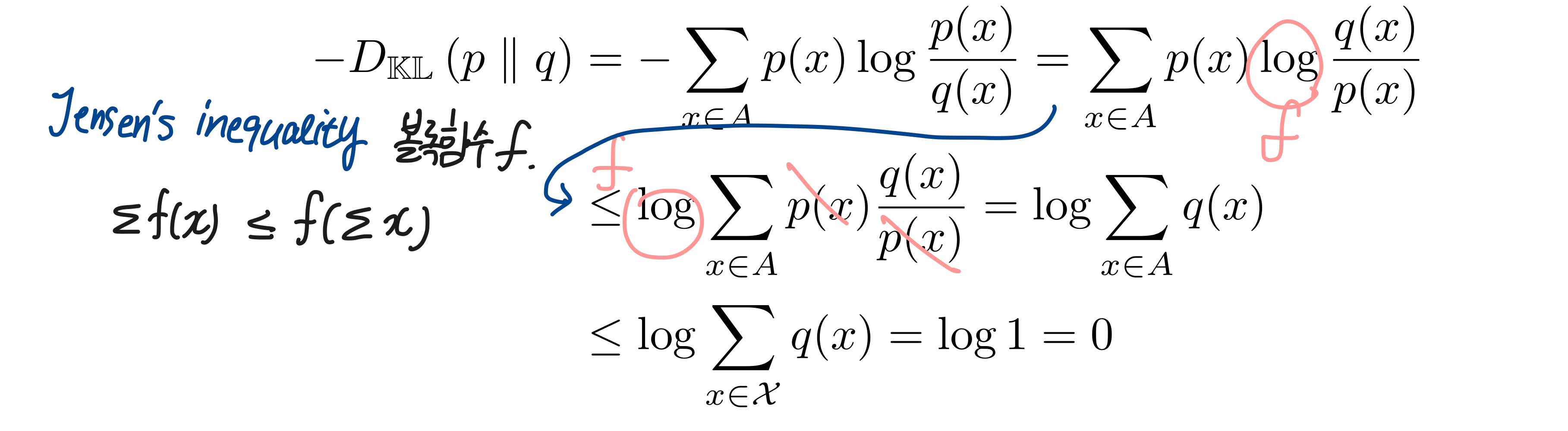
KL Divergence & MLE 

p가 정해진 분포고 이와 유사한 q를 찾고 있다 가정해 보자.  그러면 우리는 KL(p||q)가 최대한 작을  q를 구하는 것과 마찬가지다. 

p와 유사한 q 찾기

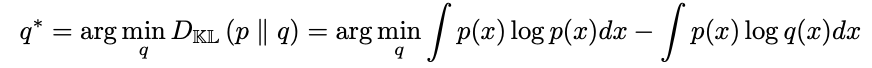
이때 첫번째 항인 p(x)logp(x) dx 는 상수로 취급할 수 있다. p가 q에 따라 변하지 않는, 정해진 분포이기 때문에 해당값은 변하지 않기 때문이다. 여기에 p의 분포가 선험적 분포라 delta function 기반이라면(값을 가진 지점에서 팍! 튀는 분포를 가지고 나머지 지점에선 0 인 분포를 생각해보자), 식은 아래와 같이 조금 더 정리가 된다. 

여기서 알 수 있는 점은 KL(p||q)를 minimize하는 것이 Likelihood(==logq(x))를 maximize하는 것과 동일하다는 것이다. 하지만 대부분의 상황에서 정답으로 간주할 정해진 분포 q가 선험적 분포를 진짜 분포로 갖고 있진 않을 것이다. (정답 분포가 특정 지점에서만 스파이크로 튀는 분포고 나머지가 0 인건 이상하긴 하다.) 이를 보완하기 위해 커널을 쓰는 방법, data augmentation 등을 쓰는 것이다.  

Forward vs Reverse KL 

이번에는 KL(p||q)와 KL(q||p)의 분포에 대해서 생각해보자. 첫 번째는 forward KL인  KL(p||q)다. KL divergence는 0에 가까울수록 p와 q의 분포가 유사하므로 이 수식에서는 q를 통해 KL을 minimize 하는 것이 목표가 된다. 만약 q(x)가 0이라면 어떨까? 그러면 log p/q 항이 inf로 가며 KL(p||q)의 값은 무한으로 커질 것이다. 그러면 q는 0보다는 커야 하는 제약을 줘야 함을 알 수 있다. 그리고 q는 분모의 위치에 있으므로 분자 p를 포함하는 분포로 가려는 경향이 생긴다. 

forward KL

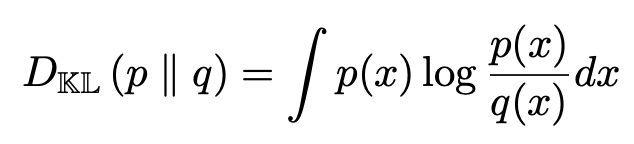
반대로 reverse KL KL(q||p)는 어떻게 해석할 수 있을까? q를 조절하여 KL값을 minimize하는 것은 여전히 같은 목표다. log p/q값이 무한대로 튀지 않게 하기 위해 이번엔 p(x)가 0만 아니면 된다. p(x) > 0을 만족하며 q가 작을수록 KL 값은 줄어들게 된다. forward KL과는 반대로, q는 p를 포함하는 분포로 가지 않아도 KL을 작게 만들 수 있다. ELBO를 구할 때 와 같이 KL divergnece를 사용하는 경우에서 KL은 이 reverse KL을 사용하곤 한다.

reverse KL

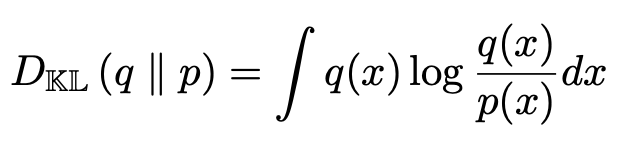
실제분포 p가 bimodal일 때 forward와 reverse KL로 q가 어떤 분포를 따라가는지 아래 그림을 통해 확연히 확인가능하다. (a)가 forward KL, (b),(c)가 reverse KL일 때로 빨간색이 q의 분포를 나타내고 있다.  

bimodal q with unimodal p (forward, reverse KL)

 

3. Mutual Information

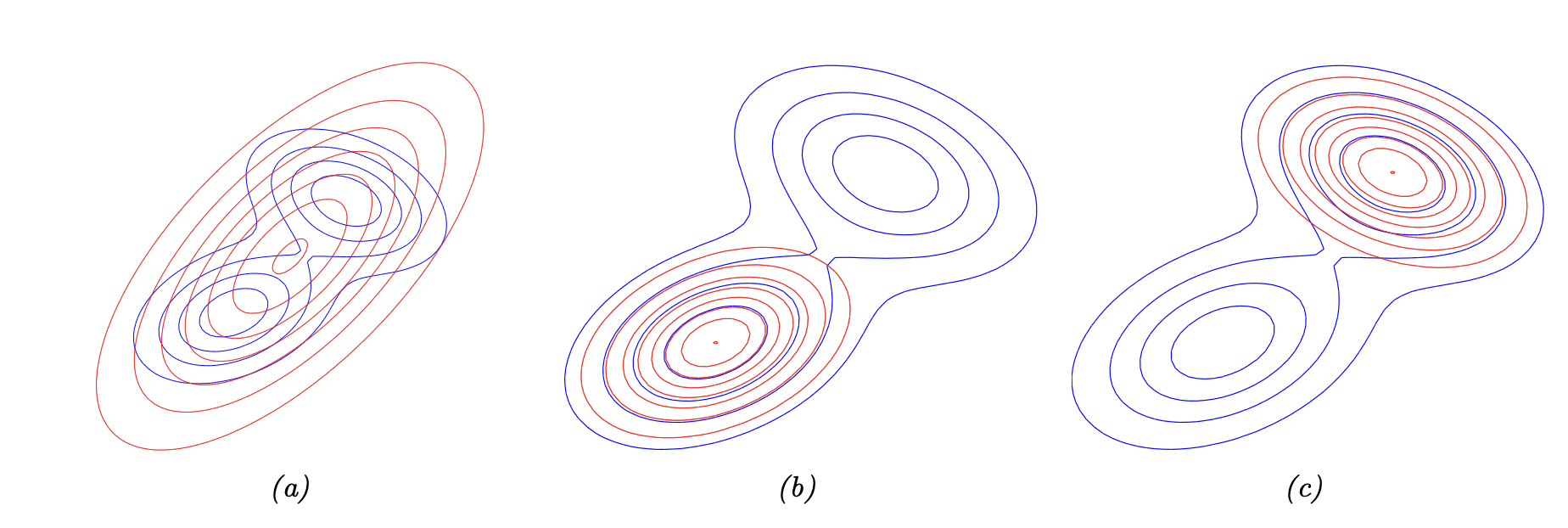
지난 글에서 KL-divergence는 p와 q가 얼마나 유사한지를 판단할 수 있는 척도였다. 0 일수록 유사하고 값이 클수록 유사하지 않음을 알 수 있었다. Mutual Information(MI)는 p와 q의 유사함보다는, 둘의 의존성에 대해 알 수 있다. 두 변수 x와 y의 MI는 I(x;y)로 나타내는데 이를 통해 x와 y가 얼마나 dependent 한 지를 구할 수 있다.

x와 y의 dependency를 보고 싶기 때문에 x과 y의 joint probability P(x,y)를 통해 P(x), P(y)와의 유사함을 나타내는 식을 그릴 수 있다. 유사성을 보기 위해서 우리는 KL Divergence를 이용할 수 있음을 알고 있다. 이번에도 적용해 보자. 

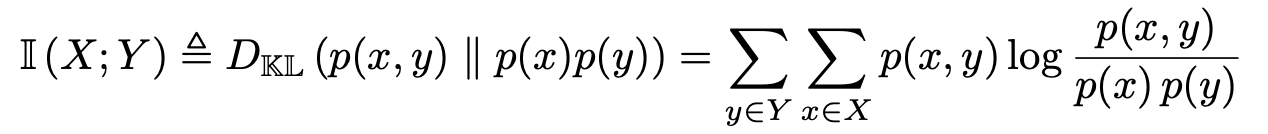
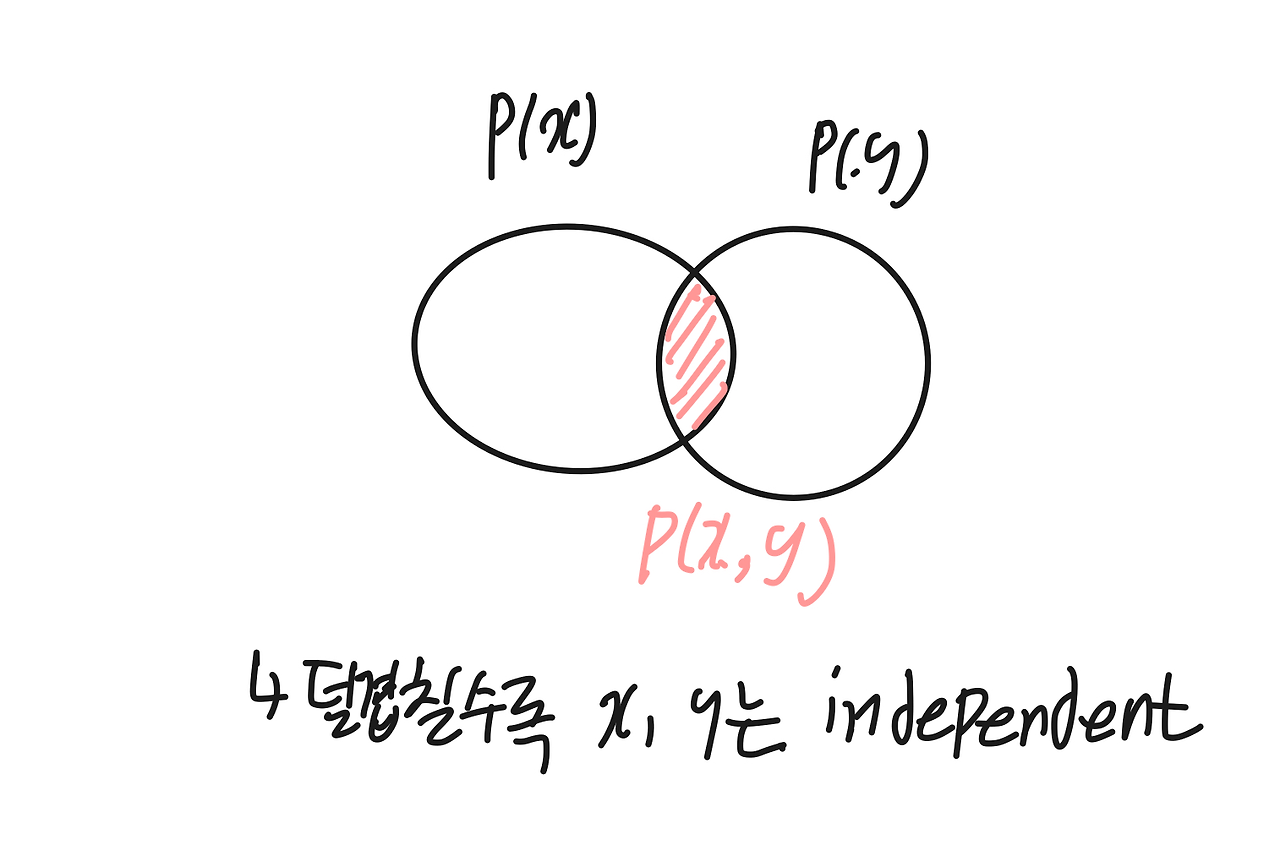
아래의 밴다이어그램을 통해 유사성을 보려면 p(x,y)가 p(x)p(y)와 멀어질수록 좋음을 알 수 있다.

x와 y가 dependent 할 수록 P(x,y)가 P(x)P(y)와 더욱 유사해질 것이다.  따라서 MI가 작을수록 x와 y는 independent하다. 

MI 해석

아래 엔트로피에 대한 벤다이어그램을 봤을 때 X의 엔트로피와 Y의 엔트로피의 교집합이 MI에 해당하는 것을 알 수 있다. 

(지난 내용을 recap해보자. )

• Entropy H(X) =  - ∑p(x) log p(x)
• Joint Entropy H(X,Y) = - ∑ p(x,y) log p (x,y)
• Conditional Entropy H(X|Y) = H(X,Y) - H(Y)

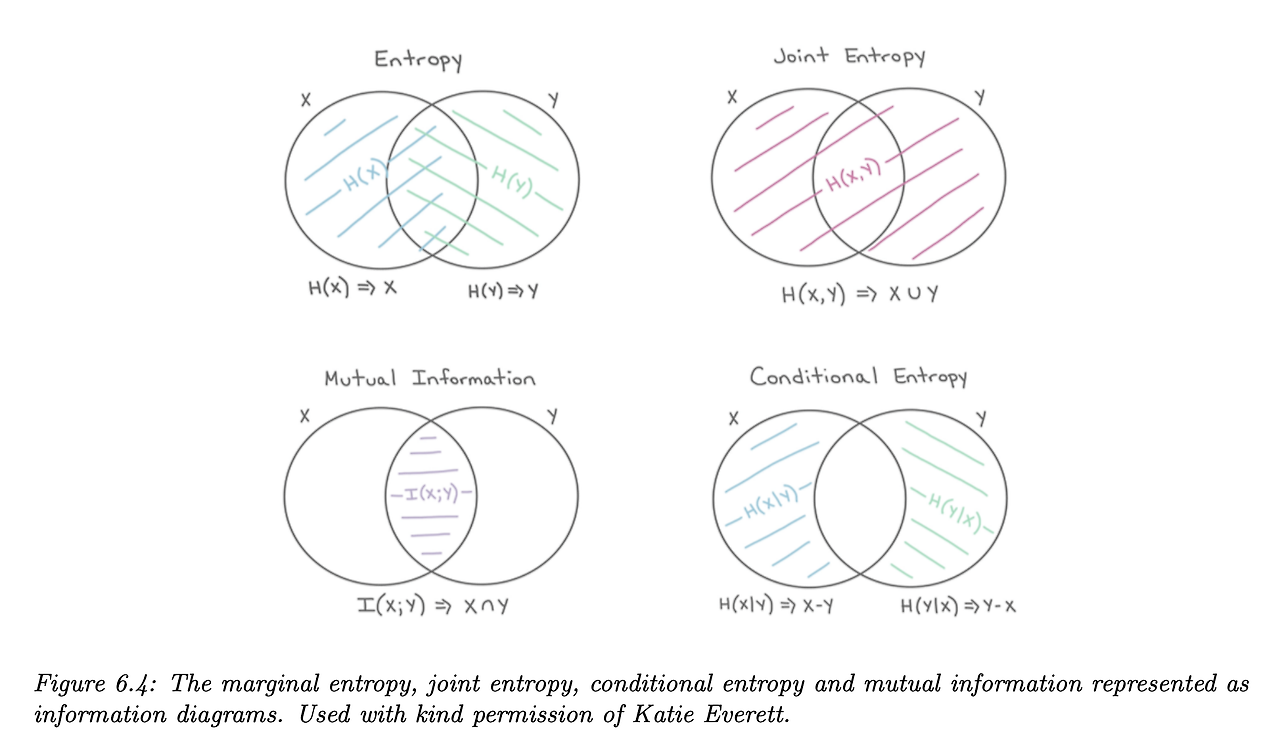
위 그림에서 2가지 MI 수식을 유추할 수 있는데,

1. MI는 Entropy(첫 번째 벤다이어그램) - Joint Entropy(2번째 벤다이어그램)으로 볼 수 있다.

$$ I(X;Y) = H(X) + H(Y) - H(X,Y) $$

2. MI는 각 Entropy(X) - Conditional Entropy(X|Y)로도 해석할 수 있다. 

$$  I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) $$

Normalized MI

지난 글에서 증명한 엔트로피의 성질에 따라 H(X,Y) = H(X|Y) + H(Y) = H(Y|X) + H(X)를 생각해 보면 식은 더 단순해진다. 

$$  I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) $$

위 식을 봤을 때 알 수 있는 점은 I(X;Y)는 항상 H(X) 또는 H(Y)보다는 작을 것이란 거다. 즉 I(X;Y) <= min(H(X), H(Y))가 성립한다! 이렇기 때문에 만약 I(X;Y)를 0~ 1사이로 normalize 하고 싶다면 min(H(X),H(Y))로 나눠주면 되며, 이때는 Normalized Mutual Information(NMI)라고 쓴다. MI는 KL divergence 기반이기 때문에 어차피 0보다는 크다.

Normalized Mutual Information

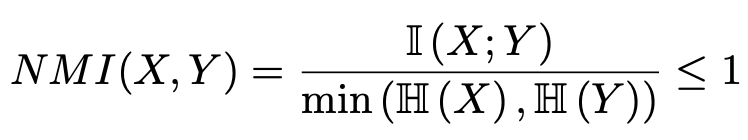
만약 NMI(X;Y)가 1이고 min(H(X), H(Y)) = H(X)라면, H(X|Y) = 0을 의미한다. conditional entropy H(X|Y)가 0이란 뜻은 H(Y)가 H(X)에 무조건 속하는 상태로도 해석할 수 있다. 따라서 NMI값이 1이란 뜻은 두 변수 중 하나가 무조건 상대 엔트로피의 포함관계인 것이다.

2. conditional mutual information

 

[위키피디아] Conditional Mutual Information

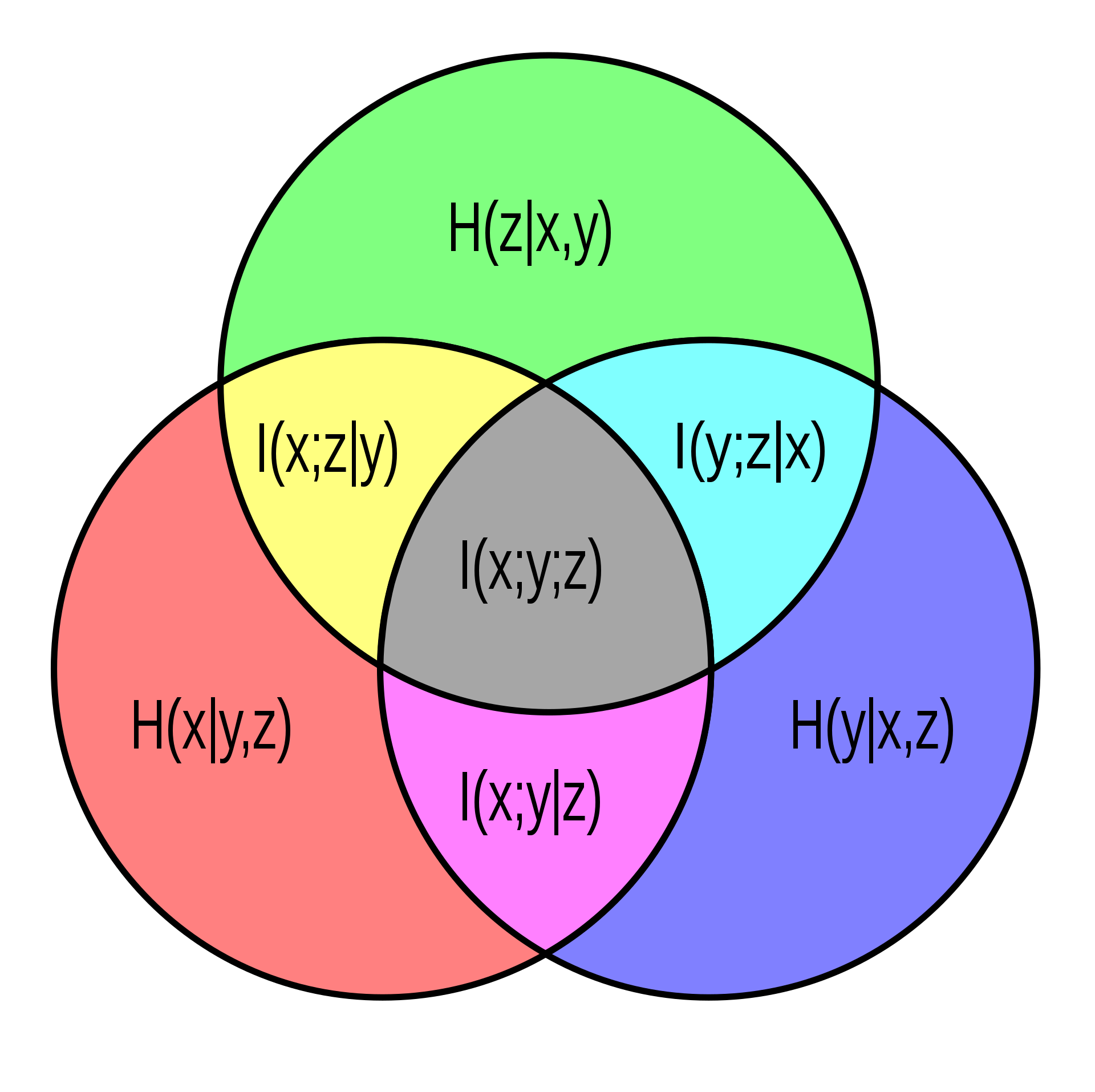
이번엔 conditional MI를 통해 MI에도 chain rule이 적용됨을 보일 것이다. 아래와 같이 Z가 주어졌을 때의 X와 Y의 MI를 전개해 보자. 

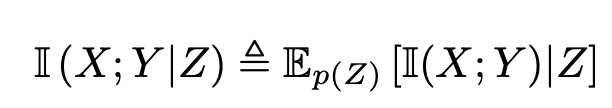
우변을 풀어써보면 다음과 같다. 

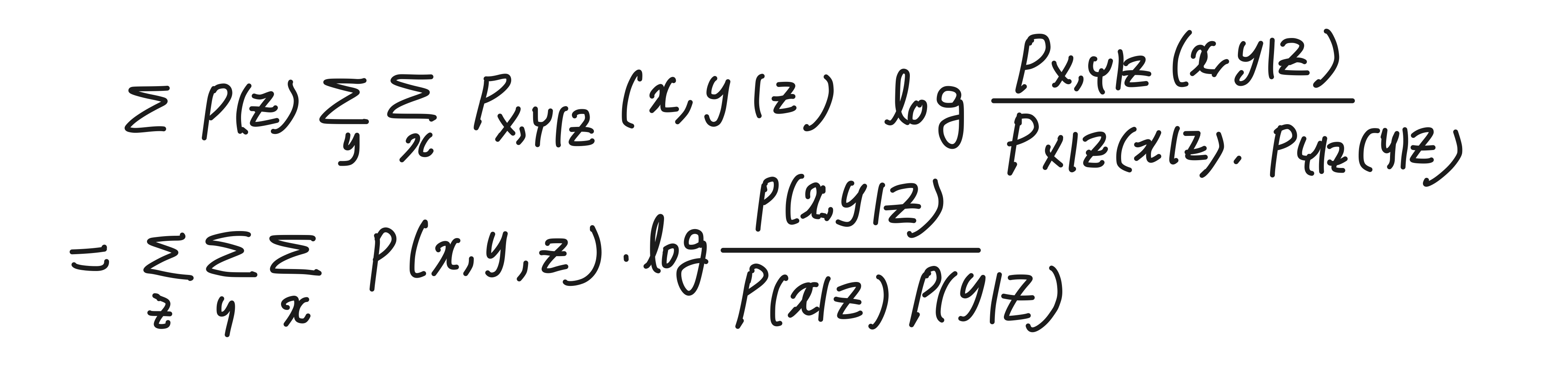
식이 얼추 정리가 되었으니 log 를 풀어서 entropy H 형태로 정리해 보자. conditional prob들을 다 joint로 풀어냈다.(책과는 다르게 풀었다.)

이제 이 식을 MI 식으로 묶어볼 수 있다. 

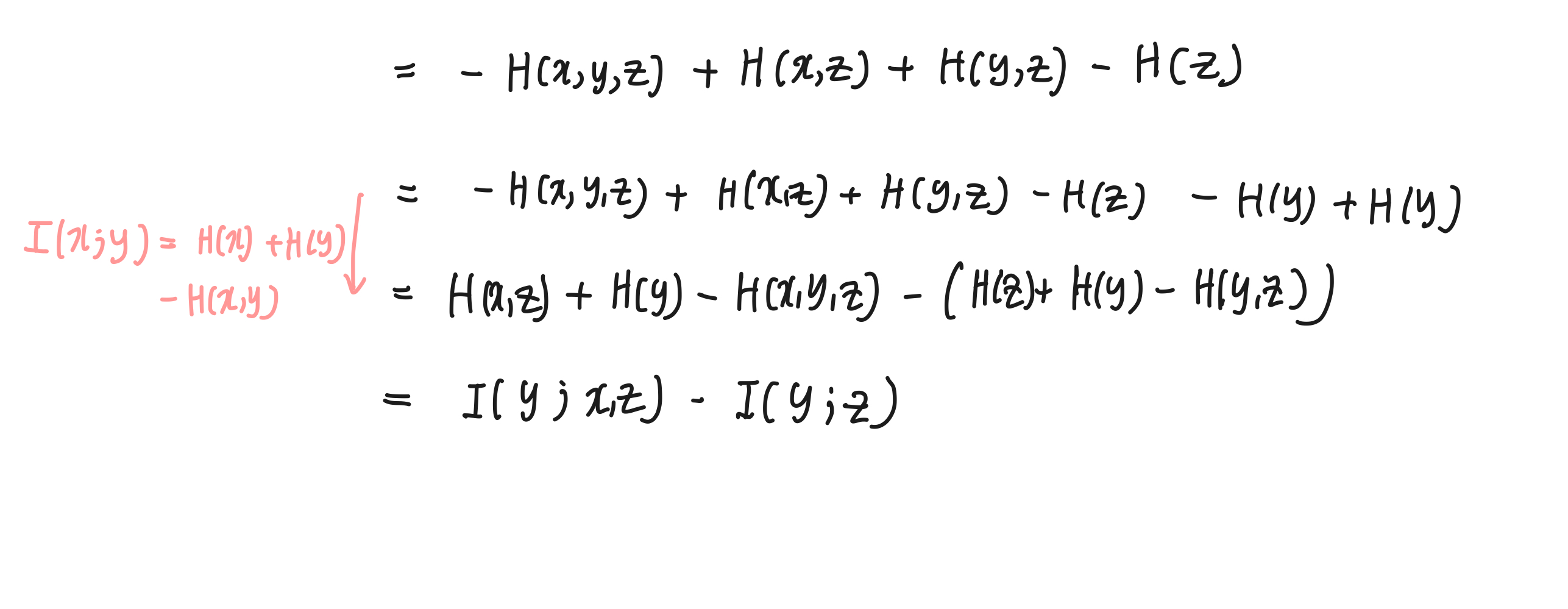
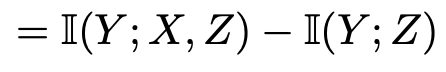
따라서 I(X;Y|Z) = I(Y;X,Z) - I(Y;Z) 임을 보였다. 만약 위 식에서 H(y)가 아닌 H(x)를 더하고 뺐다면 식은 이렇게도 정리가 가능하다. 

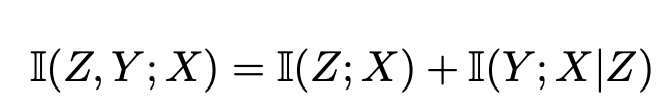
이 식에서 Z에 Z1를, Y에 Z2를 각각 대입해 보면 chain rule이 성립하겠구나를 알 수 있다. 따라서 아래와 같이 Mutual Infromation에서 Chain rule을 구할 수 있다!

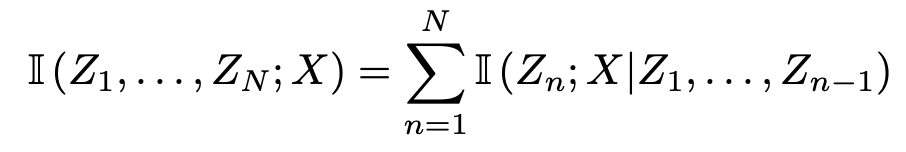
3. joint gaussian일 때 

이번엔 분포 x, y가 join gaussian distribution을 따른다고 가정해 본다. 그러면 두 분포의 gaussian은 아래와 같이 표현되는데, 이때 ρ는 둘의 상관계수다.

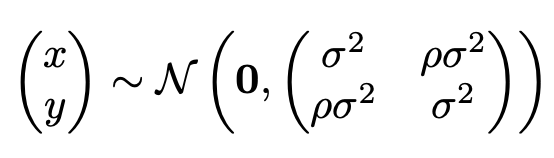
이때의 MI(x;y)를 구해보자. 먼저 평범한 1 dimension gaussian distribution x의 엔트로피 식은 다음과 같으며, u는 평균을 의미한다. 

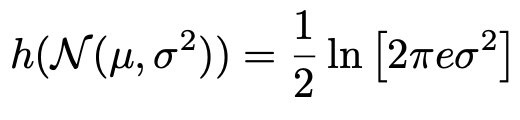
이 식의 σ 자리에는 joint distribution의 분산이 자리하면 되기 때문에, det(∑)가 자리하게 된다. det(A) = ad- bc였음을 기억하면 X,Y의 joint entropy h(X,Y)는 아래와 같이 정리된다. 

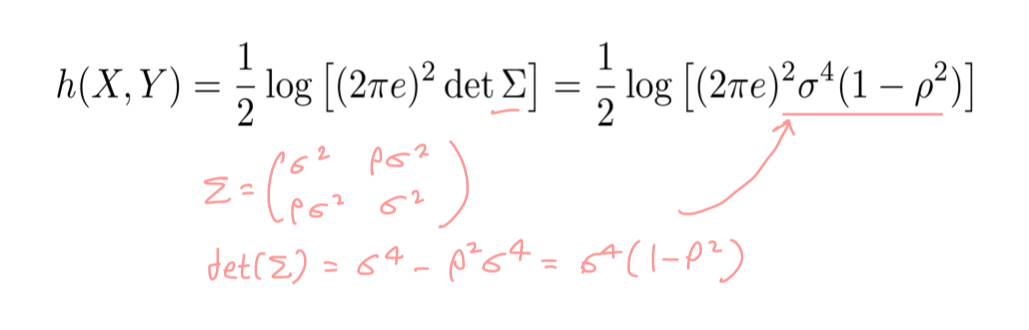
I(X,Y) 는 H(X) + H(Y) - H(X,Y)였다. 각 자리에 대입해 보자. 

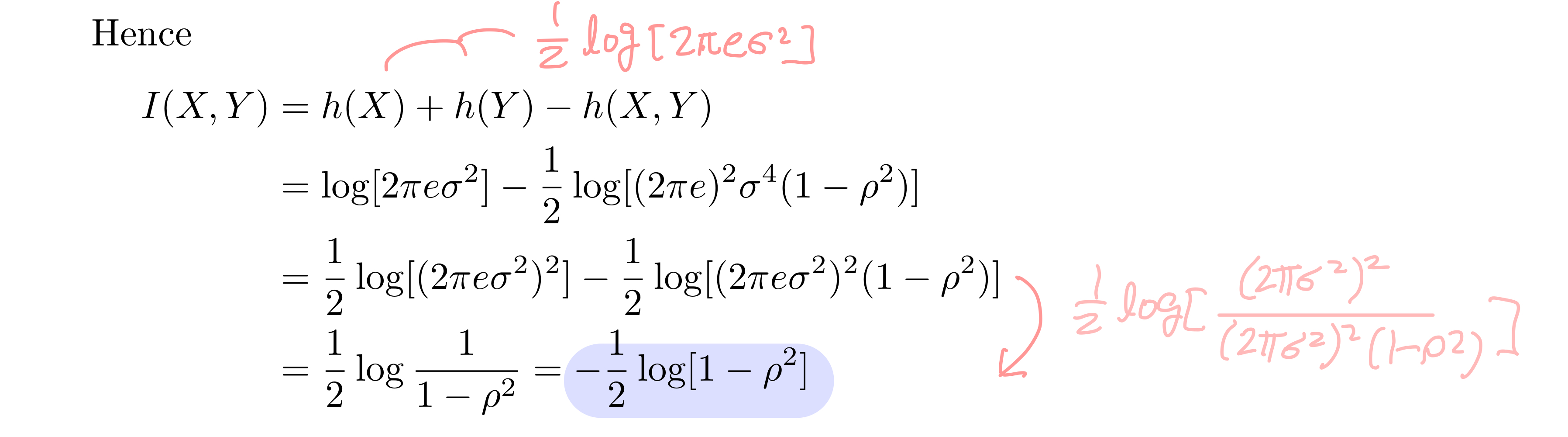
식이 정리가 됐다. 이로써 join gaussian distribution인 둘의 MI는 상관계수 ρ로 인해 정해짐을 알 수 있다. 이제 ρ자리에 1, -1, 0을 대입해 보며 MI가 어떻게 될지 보자.

• ρ = 1 :  I(X,Y)는 무한대로 가며 둘의 joint covariance(∑) 도 양수다. 이는 Y가 X에 대해 무한대로 정보를 갖고 있음을 뜻한다. 
• ρ = 0: I(X,Y)값이 log 1로 0이다. 즉 X, Y는 연관성이 전혀 없다. 
• ρ = -1 :  I(X,Y)는 무한대로 가는데 둘은 음의 상관성, X = -Y를 만족할 것이다.

4. MIC

x, y가  discrete 하지도, 그렇다고 gaussian 과 같이 해석가능한 continuous 분포도 아닌 real-valued data (continuous) 라면 NMI를 구하는 게 조금 까다롭다. 이럴 땐 continuous한 variable들을 구간별로 쪼개서 구할 수 있다. 각 구간별로 information 계수를 구한 후 이 구간들 중 가장 큰 값을 가진 계수를 택하는데 그래서 이름이 Maximal Information Coefficient(MIC)이다. 

식을 볼 때 G는 격자로 자른 구간을 의미한다. 구간들 각각 MI를 구하고, 그중 가장 큰 MI를 가진 구간의 MI를 MIC로 정의하고 있다. 

MIC 수식

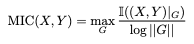
 MI의 특징 상 MIC가 0이라면 x, y간 어떤 관계도 없음을(independent), 1이라면 noise-free한 관계를 가짐을 알 수 있다. 변수간 상관성을 보는 방법으로는 상관계수(Correlation Coefficient. corr)도 있다. MIC는 상관계수와 다르게 linear한 관계만을 보지도 않는다. 그렇기 때문에 corr을 구하는 대신 MIC를 보는 것이 유용할 때도 있다. 예를 들어 아래의 그림에서 E,F,G는 각각 2개의 변수에 대한 계수를 구한 지점이다. 각각 상관계수가 0에 가깝지만 MIC를 봤을 땐 0.5보다 크므로, 선형적인 상관성은 없을지 몰라도(corr = 0) 실제로는 상관성이 있다. 

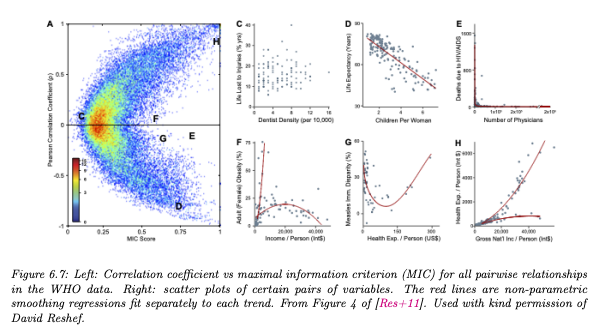
5. data processing inequality

어떤 변수 X가 Y라는 함수를 통해 Z로 변환된다면(X -> Y -> Z), I(X;Y) >= I(X;Z)가 성립한다. 직관적으로 볼 때 X와 Y의 연관성이 X와 Z의 연관성보다는 높을 거라는 결론이 나올 수 있는데, 위 conditional mutual information 증명 과정에서 조금 변형하면 수식적으로도 증명할 수 있다. 

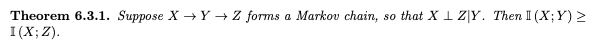
증명을 해보자면 다음과 같이 I(X;Y,Z) = I(X;Z) + I(X;Y|Z)를 도출할 수 있다. 

여기서 Z와 Y의 자리를 바꾸면 I(X;Y,Z) = I(X;Y) + I(X;Z|Y)도 성립한다.

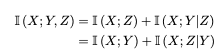
X와 Z|Y는 직교한다고 가정했기 때문에 I(X; Z|Y) = 0일 것이고, I(X;Y|Z)는 항상 0보다 같거나 크기 때문에(KL divergence의 성질. 항상 0보다 크다.), I(X;Y) > I(X;Z)로 표현할 수 있게 된다! 

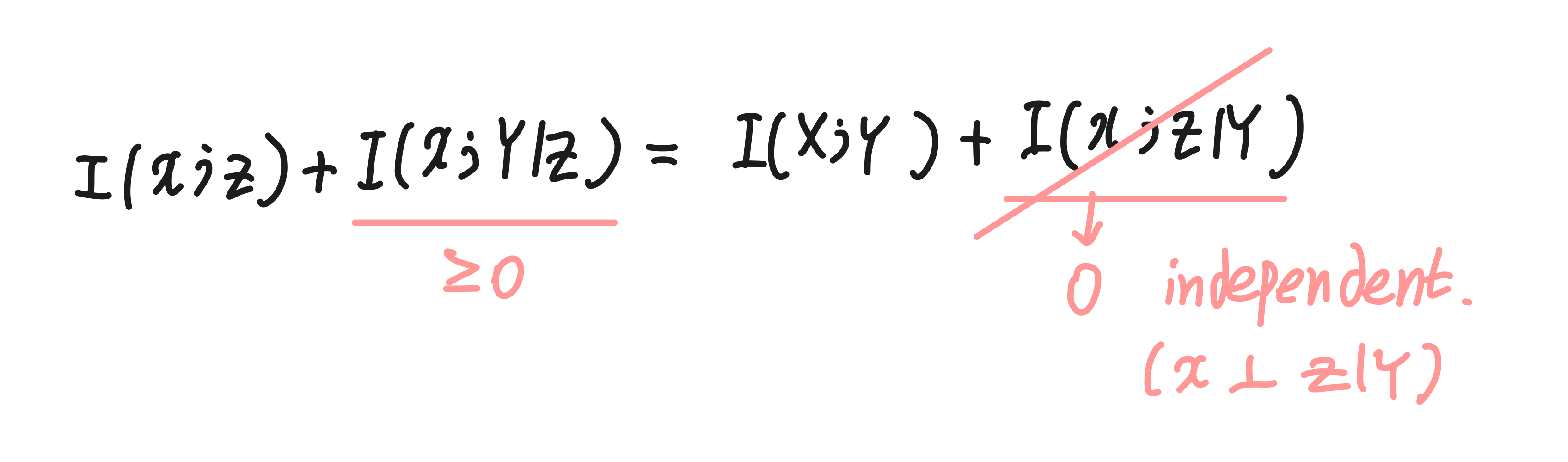
6. Fano's inequality

MI가 두 변수에 대한 상관성을 측정하기 때문에 feature selection에서도 유용하게 사용될 거다. 특정 피쳐 X와 클래스 라벨 Y 간의 상관성을 볼 때(이때 X가 예측한 Y는 Y^라고 하자), X와 Y의 상관성이 높은데 Y와  잘못 예측한 값과의 상관성은 더 높게 나오면 어떡할까?

다행히도 이런 일은 없다. 잘못 예측한 경우의 엔트로피가 항상 더 크기 때문인데,  이를 fano's inequality라고 한다. 지금부터는 이를 증명해 볼 것이다. 

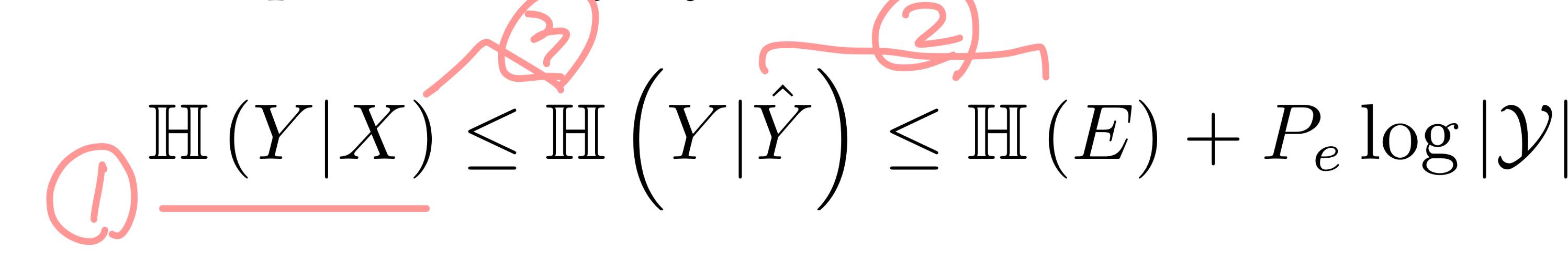
전제 - 우선 에러 E는 실제 라벨 Y와 예측값 Y^이 다를 경우로, 이때의 확률을 Pe = P(Y != Y^)라고 나타내겠다. 에러가 날 확률의 minimum boundary를 H(Y|X) 통해 구해보자. (참고로 우리가 feature selection에서 높은지 알고 싶은 MI는 I(X;Y) =  H(Y) - H(Y|X) 로 표현할 수 있었기 때문에 H(Y|X)가 낮아질수록 I(X;Y)는 높아진다. )

1 - 첫 번째로는 H(Y|X)가 어떤 의미를 가지는지 알아보자.

먼저, 엔트로피는 항상 1보다 같거나 작기 때문에 H(Y|X) <= 1이 성립한다. 우변에 양수인 무언갈 더한다고 해도 부등호는 달라지지 않을 것이다. 그 무언가는 여기서 Pe log|Y|가 된다. (|Y|는 클래스라벨 종류 수를 의미한다.)

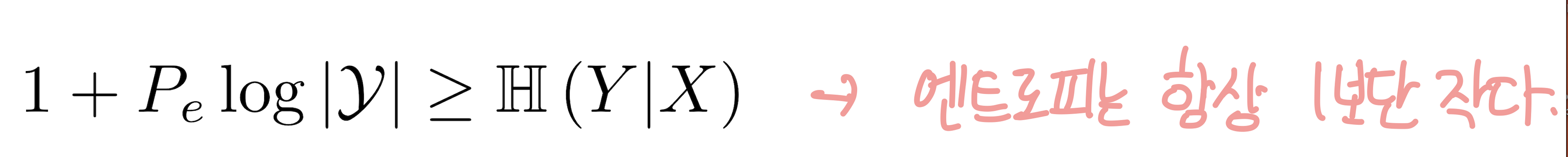
여기서 Pe에 대해 식을 정리해 보면 H(Y|X)에 따라 Pe의 최소 boundary가 지정됨을 알 수 있다. 따라서 H(Y|X)가 낮아질수록, 즉 I(X;Y)가 커질수록 에러 확률 Pe의 miminum도 낮아진다.

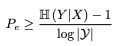
2 - 두 번째로는 H(Y|Y^) <= H(E) + Pe log|Y|임을 증명해 보자.  여기서는 H(Y2,Y1|Y0) = H(Y1|Y0) + H(Y2|Y1,Y0)인 chain rule을 사용한다. 

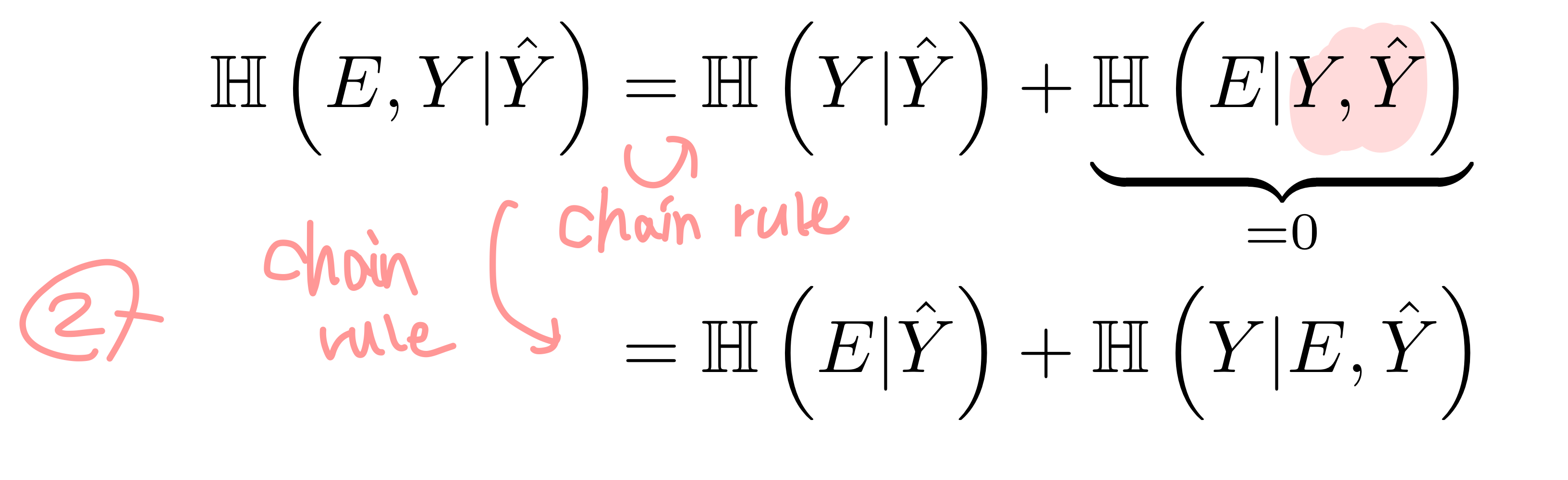
두 개를 더하면 H(Y|Y^) = H(E|Y^) + H(Y|E,Y^)를 도출할 수 있다. 여기서 H(Y|E,Y^)는 아래와 같이 상한선이 생긴다. 

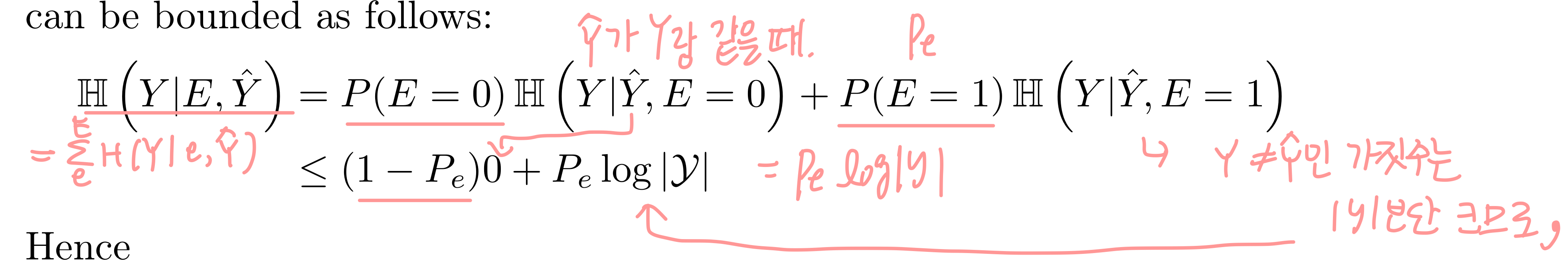
이 H(Y|E,Y^)를 H(Y|Y^) = H(E|Y^) + H(Y|E,Y^)에 대입하면 아래와 같이 되는데, 그렇기 때문에 에러의 엔트로피가 X와 Y의 엔트로피보다 크다. 

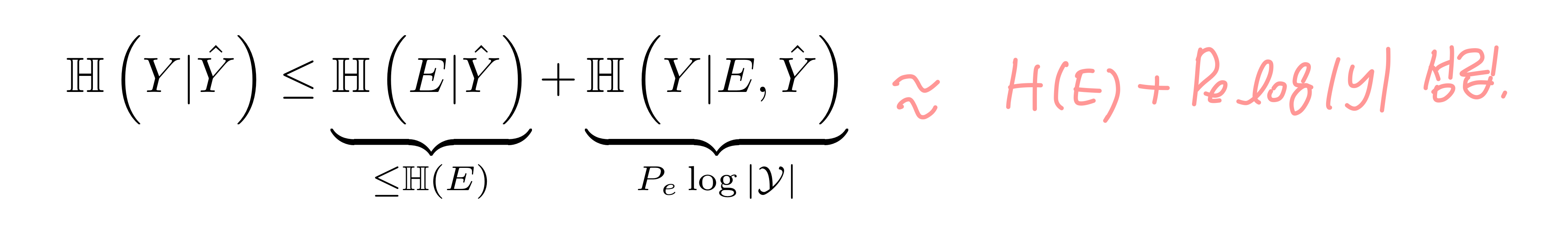
3 - 마지막으로 data processing inequality로 인해  I(Y;Y^) <= I(Y;X)이다.(Y -> X -> Y^인 셈.)  H(Y|X) < H(Y|Y^)도 성립한다. 

이로써 Fano's inequality를 증명했다. 

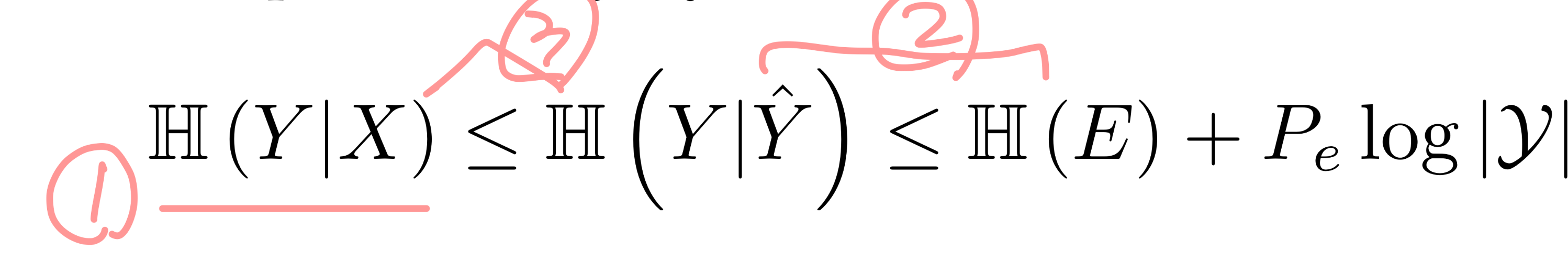
오늘은 MI가 x, y의 dependence를 측정하는 방법론으로 KL divergence를 통해 수식이 생겨먹었다는 것을 알았다. 그리고 NMI, Conditional MI를 통한 chain rule, 두 변수가 joint gaussian distribution일 땐 어떻게 MI가 전개되고 해석할 수 있는지를 알아보았다. MI가 높으면 dependence가 높은 변수인 것이기 때문에, feature selection 시에도 MI가 높은 변수를 고르는 등 사용된다. 

지난 글부터 오늘 글을 통해 entropy - KL divergence - MI 까지 완전 정복해 보았다. (그리고 정말 새삼 책이 썩 친절하지는 않구나를 느꼈다..) 코로나에 걸려서 이번주는 스킵할 뻔했는데, 저번에 써둔 글이 있어 이번주도 이렇게 완료한다. 

참고

•