[Robotics] Modern Robotics : Mechanics, planning, and control - Chapter2. Configuration Space

용어 정리

• Link : 일반적으로 Rigid 한 바디로 여겨진다.
• Joint : 링크들을 연결해주는 관절로 다양한 종류의 조인트가 존재한다.
• Actuator : 전기모터나 피스톤 등 우리가 능동적으로 움직이게 할 수 있는 부품으로 힘이나 토크를 발생시켜 링크와 조인트들을 움직이게 한다.
• End-effector : 실질적으로 필요한 Task를 수행하는 파트로써 그리퍼, 핸드 등이 여기에 속한다.
• Configuration: 로봇의 모든 지점의 위치 정보이다.
  • Planar rigid body: 2차원 상의 Configuration
  • Spatial rigid body: 3차원 상의 Configuration
• Configuration space (C-space): 로봇의 위치를 정의할 수 있는 파라미터들이 이루는 n차원의 공간이다.
• Degrees of freedom (DoF): 로봇의 Configuration을 표현할 수 있는 가장 작은 수의 좌표계, Grubler's formula로 계산가능.
• Topologically Equivalent: 자르거나 붙이는 것 없이 부드럽게 다른 공간으로 변형이 가능한 경우
• Task Space : 로봇의 작업을 자연스럽게 할 수 있는 공간으로, 로봇이 아닌 작업에 중점을 둡니다.
• Work Space : 로봇의 작업과 관계없이 end-effector가 닿을 수 있는 공간을 말합니다.

2.1 Degrees of Freedom of a Rigid Body

로봇에 대한 가장 기본적인 질문이 무엇일까? ‘로봇이 어디에 있는가?’이다.
이때 필요한 것이 로봇의 위치(Configuration)이다.
참고로, 이 강의에서는 로봇의 몸체가 단단한 물체(강체, rigid body)인 상태에 대해서만 다룬다.

각 링크들의 모양을 알고 Rigid하다고 가정하기 때문에 몇 개의 포인트들을 지정하여 그 곳의 위치를 알 수 있다면, 로봇의 모든 위치 정보를 얻어낼 수 있다.

Modern Robotics Figure 2.1: DoF of a Rigid Body

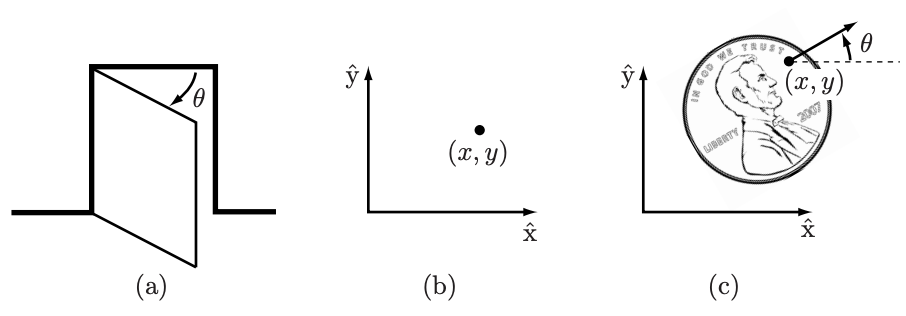
예를 들어, 문의 Configuration은 조인트의 각도 θ만 알면 모든 위치를 표현할 수 있고
평면 상의 어떤 점은 x,y 두 개의 좌표로 표현이 가능하다.
또한 테이블 위에 놓여있는 동전은 동전 위 임의의 점의 좌표와 동전의 회전 각도로 표현할 수 있다.

여기서 자유도 ​Degrees of freedom(DoF)라는 용어가 나오는데, DoF란 로봇의 Configuration을 표현할 수 있는 가장 작은 수의 좌표계를 말한다. 즉 위 사진에서 문은 1-DoF, 평면상의 점은 2-DoF, 테이블 위의 동전은 3-DoF이고 각각 1차원, 2차원 3차원의 좌표계에서 표현이 가능하다. 이렇게 로봇의 위치를 정의할 수 있는 파라미터들이 이루는 n차원의 공간을 Configuration space(C-space)라고 부른다.

Modern Robotics Figure 2.2: DoF of a Rigid Body

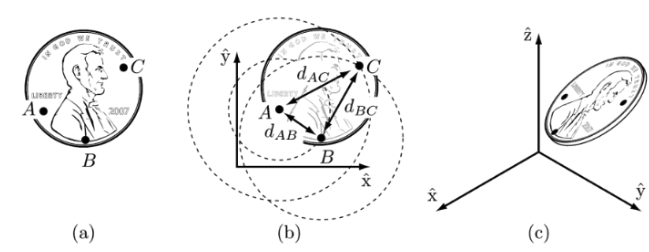
점 A, B, C는 모두 각각 2개의 좌표(값)로 표현가능하다. {(xA, yA), (xB, yB), (xC, yC)}
6개의 임의의 값(독립적인 값, independent)으로 동전의 위치를 정할 수 있기에 6-DoF를 갖는다.
하지만 동전은 강체(rigid)이므로 A가 정해지면 A,B 간의 거리인 d(A, B)가 일정함에 의해 B의 위치가 제한(constraint)된다.
그 위치는 A를 중심으로 하고 반지름의 dAB인 원 위이죠. 이때 B의 위치는 ΦAB(AB벡터와 x축 벡터가 이루는 각)하나로 표현이 가능합니다. 이후 점 C의 위치는 원AC, 원BC의 두 교점에서 가능한데, 이는 동전의 앞, 뒤에 따른 것이므로 사전에 동전의 면을 지정하면 C의 위치가 하나로 정해진다(C is fixed).
따라서 동전의 평면에서의 위치(configuration)는 (xA, yA, ΦAB) 이렇게 표현이 가능하고 3-DoF를 갖는다.

따라서 우리는 Rigid body의 자유도를 다음과 같이 정의할 수 있다.

Degrees of Freedom = (number of variables) - (number of independent equations)

위의 예를 적용시켜보면 동전 위 지점들의 자유도 합은 A, B, C 모두 x, y값을 가지므로 2+2+2 = 6의 자유도를 갖는다.
한편 A가 정해지면 B는 A에 의해 d(A,B)라는 1개의 constraint가 생기고, 마찬가지로 C는 A, B에 의해 d(C,A), d(C,B)라는 2개의 constraints가 생긴다. 따라서 1+2 = 3의 constraints(제한)이 있어 평면 위 동전의 자유도(dof)는 6-3 = 3이 되는 것이다.

2.2 Degrees of Freedom of a Robot

로봇은 몸체인 link와 관절인 joint로 구성되어 있으며, Joint는 강체(rigid body)의 행동에 제약(constraint)을 가한다.
이런 관점에서 joint의 갯수를 통해 로봇의 DoF를 알아내는 공식인 'Grubler’s formula'를 도출해낼 수 있다.

2.2.1 Robot Joints

Figure 2.3은 로봇의 기본적인 Joint들이며, 이는 ‘두개’의 link를 연결한다.
이는 3개 이상의 link를 연결하는 것은 허용되지 않는다.

Modern Robotics Figure 2.3: Typical robot joints

Modern Robotics Table 2.1: The number of degrees of freedom f and constraints c provided by common joints.

2.2.2 Grubler's formula: Calculate Degrees of freedom(DoF)

• m = 몸체의 dof 수 (평면(planar) : 3, 공간(spatial) : 6)
• N = 로봇의 link 갯수 (ground 도 link로 친다.)
• ci = i번째 Joint의 constraint 수
• J = 로봇의 Joint 갯수
• fi = i번째 Joint의 자유도(freedom)
• ... 를 이용하여 DoF를 구하는 'Graubler's formula'는?

Modern Robotics Figure 2.4: Calculate DoF

• 여기서, 왜 ci = m - fi?
  • DoF = (number of variables) - (number of independent equations)
  • number of independent equations = (number of variables) - (DoF)

Modern Robotics Figure 2.4: linkage

Figure 2.4 (a)는 4개의 link(몸체)를 가지고(ground 포함) 4개의 revolute joint(회전 관절)를 가진다.
모든 link가 같은 평면 상에서 움직이므로 m = 3입니다.
N = 4, J = 4, fi = 1, i = 1,…,4를 Grubler’s formula에 대입하면 (a)는 1의 dof를 갖는다는걸 알 수 있다.

Figure 2.4 (b)는 두가지 방법으로 해석이 가능하며, 두가지 방법 모두에서 메커니즘은 1-DoF를 가진다.

1. 3개의 revolute joint와 1개의 prismatic joint를 가지고(J = 4, 각 fi = 1) 4개의 link로 구성되어 있다(N = 4, ground link 포함).
2. 2개의 revolute joint (fi = 1)와 1개의 RP joint(revolute and prismatic joint의 약자, fi = 2)를 가지고 3개의 link로 이루어져 있다(N = 3; 각 joint는 2개의 link만을 연결해야 하기 때문).

2.3 Configuration Space: Topology and Representation

2.3.1 Configuration Space Topology

로봇의 위치에 대해 표현할 때에, dof와 c-space에 대해 아는것 외에도 '공간의 형태(Shape)'에 대해서도 알아야 한다.

우리가 구형인 지구본에서 위치를 표현할 때, 주로 위도와 경도 두가지 coordinate를 사용하여 위치를 표현하며, 평면 공간의 위치를 표현할 때에도 x,y의 두가지 coordinate를 사용하여 위치를 표현한다. 하지만 구의 표면과 평면공간은 둘 다 동일한 2차원이라고 할 수는 없으며, 엄연히 평면과 구는 같은 형태(shape)가 아니기에 이를 구분해야 한다.
여기서 공간의 형태가 다르다는 말은 서로 Topologically Distinct하다고 하며, 이와 반대로 자르거나 붙이는 것 없이 부드럽게 다른공간으로 변형이 가능한 경우를 Topologically Equivalent 라고 한다.

위상적으로 구분되는(Topologically Distinct) 1차원 공간으로는 원, 직선, 닫힌 구간의 선분이 있다.
원: S 또는 S^1라고 표기하며 1차원의 구(Sphere)라는 뜻이다.
직선: E 또는 E^1라고 표기하며 1차원의 유클리드 공간(Euclidean space)라는 뜻이다.
닫힌 구간의 선분: 보통 실수(Real number)로 표현되기에 R 또는 R^1으로 표기한다.

이때, 공간의 위상 (Topology of space)은 공간 자체의 근본적인 성질이며, 우리가 공간의 한 점을 표현하기 위해 어떤 coordinate를 선택하는지와 관계없이 독립적인 성질이다.

예를 들어 한 원에서 위치를 표현할 때에 원의 중심을 기준으로 θ값으로 나타낼 수도 있고 reference frame을 선택해 x,y의 두 coordinate로 좌표를 나타낼 수 있으나, 어떤 방법을 선택하든 공간의 위상 자체는 변화하지 않는다.

따라서 아래의 사진을 보면 평면공간, 구, 2R robot arm, rotatimg sliding knob의 c-space들은 모두 2개의 coordinate로 표현이 가능하지만 위상(Topology)는 모두 다름을 확인 할 수 있다. 이때, 2개의 coordinate를 사용하여 topology를 표현하려고 하면 각각의 특이점과 불연속인 부분이 존재한다. 

Modern Robotics Table 2.2: Four topologically different two-dimensional C-spaces and example coordinate representations

2.3.2 Configuration Space Representation

위처럼 위상(topology)를 Euclidean 좌표계에서 coordinate를 사용하려 표현하려고 하면 특이점과, 불연속인 부분이 생기는 이유는 Euclidean좌표계의 공간과 구, 2R robot arm, rotatimg sliding knob 등 각각의 c-space들은 다른 위상(topology)를 가지고 있기 때문이다.

따라서 다른 방법으로 공간을 표현(Implicit representation)할 수 있어야 하며, 현재까지의 방법(Explicit parametrization)과 비교해 보려고 한다. 

Explicit parametrization는 n차원의 공간을 n개의 coordinate만으로 표현하는 방법으로, 이는 구의 경우 위도와 경도라는 두가지 coordinate만으로 표현이 가능하다는 장점이 있지만, 위도가 낮은 곳과 높은 곳의 coordinate의 변화량의 차이가 크고, 북극점 남극점과 같은 곳에서는 잠깐 옆으로만 가도 값이 180도 달라지는 특이점과 불연속한 점과 같은 문제가 발생한다.

​Implicit representation은 n차원의 공간을 n차원 이상의 Euclidean공간(n+1개의 parameter)에 포함된 것으로 보는 방법이다. 예를 들어 위도와 경도로 표현하는 2차원의 단위 구는 3차원 Euclidean공간에 포함된 표면으로 볼 수 있는 것이다. 이는 기존(위도,경도)보다 고차원의 공간의 coordinate(x,y,z)를 사용하는 방법입니다. coordinate의 갯수만 보면 dof가 2에서 3으로 변했다고 생각 할 수 있지만, 이때, (x^2+y^2+z^2=1)이라는 단위 원의 특성상 구의 반지름 길이에 의한 constraint가 발생하기 때문에 같은 DoF를 가진다.
따라서 이는 기존 dof의 갯수보다 더 많은 coordinate를 사용해야 하는 단점이 있지만, 특이점(singularity)가 발생하지 않는다는 장점을 가진다.

따라서 로봇의 Configuration에 대한 표현은 대체로 '​Implicit representation'를 사용하여 표현한다.

2.4 Configuration and Velocity Constraints

Figure 2.10 과 같이 closed-loops를 가진 로봇들은 implicit한 표현을 explicit한 표현보다 쉽게 얻을 수 있다.

Modern Robotics Figure 2.10: The four-bar linkage.

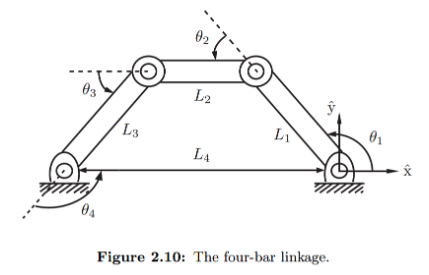
실제로 위의 그림의 경우 1-DoF를 가지고 있기에 θ 하나로 표현이 가능하지만, 이는 closed loop에서는 유도하기 어렵고, 특이점(singularity)을 가질 가능성이 있다. 이때 Implicit representation을 사용하면, 각각의 joint의 각도와 링크의 길이로 아래의 loop-closure equation을 만들 수 있다.

loop-closure equation

loop-closure equation에 대한 간단한 설명은 다음과 같으며, 자세한 설명은 하단의 링크를 참고한다.

첫번째 줄: link의 위치에 관한 식 : L1에서 L2, L3, L4를 거쳤을 때 원점에 도달함을 나타낸 식입니다.
두번째 줄: L4의 방향에 관한 식 : L4의 가리키는 방향이 L1의 시작지점과 일치함을 나타낸 식입니다.
세번째 줄: closed-loop에 관한 식
+ 참고: 2.4 Holonomic https://needs-searcher.tistory.com/78?category=921280 

2.5 Task Space and Workspace

Task Space : 로봇과 관계없이 Task를 수행할 수 있는 공간. e.g. 종이에 점을 찍는 작업의 Task Space는 R2

Work Space : 로봇의 작용점(end-effector)이 미칠 수 있는(닿을 수 있는) 공간이며, 로봇의 작업(task)에 관련없이 로봇의 구조와 관련이 있다.

Modern Robotics Figure 2.12: Examples of workspaces for various robots